二叉树的重要的遍历序列有三种:先序遍历,中序遍历,后序遍历。其中中序遍历可以由其他两种遍历序列定位的根来划分出左右两棵子树,所以已知的两种遍历序列中必须有中序遍历。
示意图(先序+中序->后序)
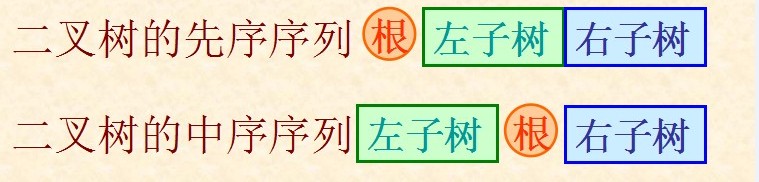
对于先序遍历序列,树根一定是第一个元素(后序遍历的根则是最后一个),知道树根后在中序遍历中找到树根,则根前面的就是左子树,后面的就是右子树,再递归的对左右子树执行上述操作直到序列为空,输出序列就是另一种序列。对于求先序序列,每次都是找到树根就输出,而求后序序列时是先递归处理完左右子树后再输出根。
代码:
输入中序和后序,求先序
输入:
DBKFIAHEJCG
DKIFBHJEGCA
输出:
ABDFKICEHJG
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 150
using namespace std;
char in[MAXN],post[MAXN];
void make_pre(char *a,char *b,int len)
{
cout<<b[len-1];
int le1 = 0,le2 = 0;
for(int i = 0;i < len;i ++,le1 ++)
if(a[i] == b[len-1])
break;
le2 = len - le1 - 1;
if(le1 > 0)
make_pre(a,b,le1);
if(le2 > 0)
make_pre(&a[le1+1],&b[le1],le2);
}
int main()
{
freopen("./tree_trans.in" , "r" , stdin);
cin>>in>>post;
make_pre(in,post,strlen(in));
return 0;
}
|
输入中序和先序,求后序
输入:
DBKFIAHEJCG
ABDFKICEHJG
输出:
DKIFBHJEGCA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 150
using namespace std;
char in[MAXN],pre[MAXN];
void make_post(char *a,char *b,int len)
{
int le1 = 0,le2 = 0;
for(int i = 0;i < len;i ++,le1 ++)
if(a[i] == b[0])
break;
le2 = len - le1 - 1;
if(le1 > 0)
make_post(a,&b[1],le1);
if(le2 > 0)
make_post(&a[le1+1],&b[le1+1],le2);
cout<<b[0];
}
int main()
{
freopen("./tree_trans.in" , "r" , stdin);
cin>>in>>pre;
make_post(in,pre,strlen(in));
return 0;
}
|
